Classical Control Theory
Tuyen D. Le April 30, 2022 [Control] #Brian-Douglas1. Background
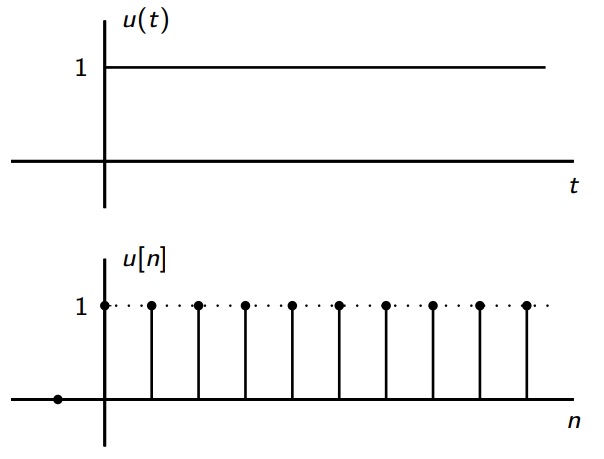
1.1. Step function
1.2. Impulse unit function (in descrete domain)
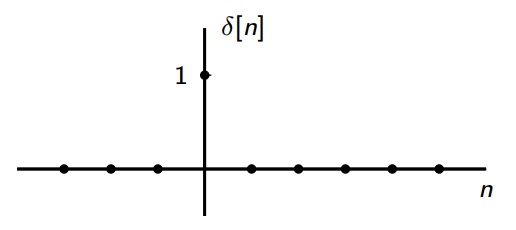
We will use this relation later on.
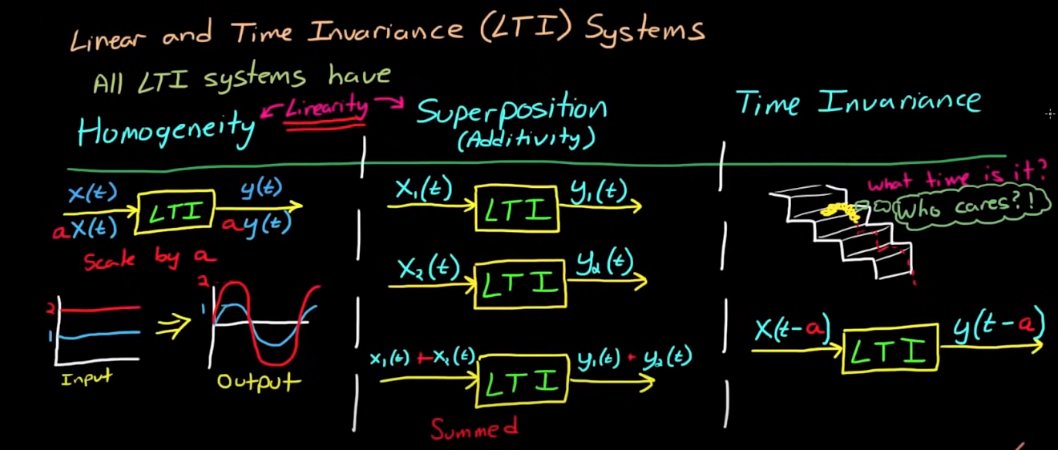
1.3. "Linear and Time Invariance" (LTI) systems
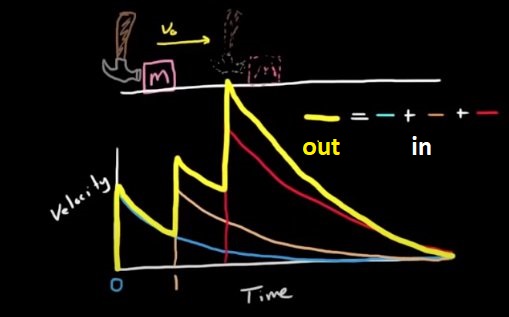
An example of LTI system.
1.4. Laplace transformation
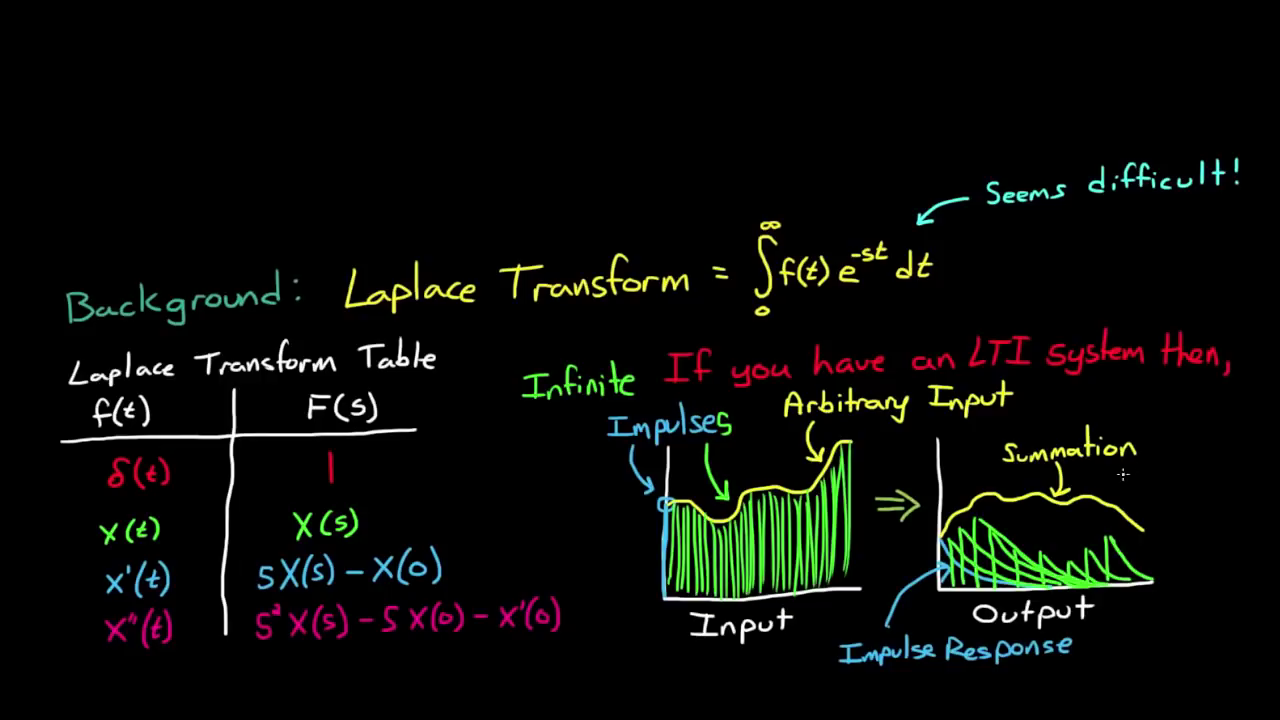
2. Transfer function
Q. What is impulse response $h[n]$ of a system?
A. When the input is a impulse unit function $\delta [n]$ (see "Impulse unit function" section above)
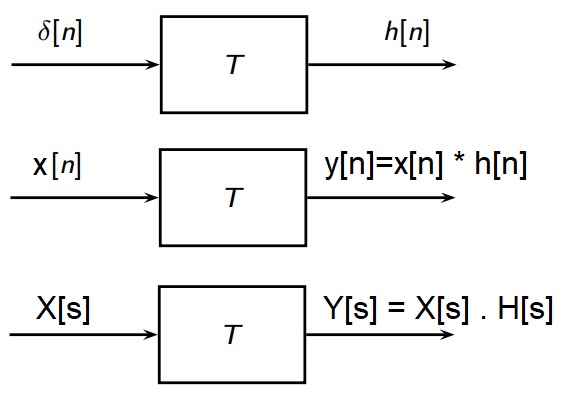
Now, if we take a Laplace transformation of $y[n]$, we have.
We call $H[s]$ is the transfer function of the system.
An example of using impulse response in the system.
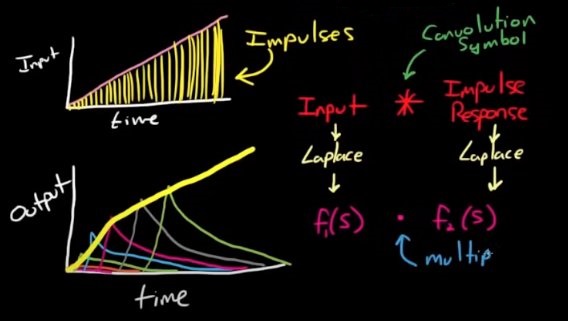
From convolution to transfer function.
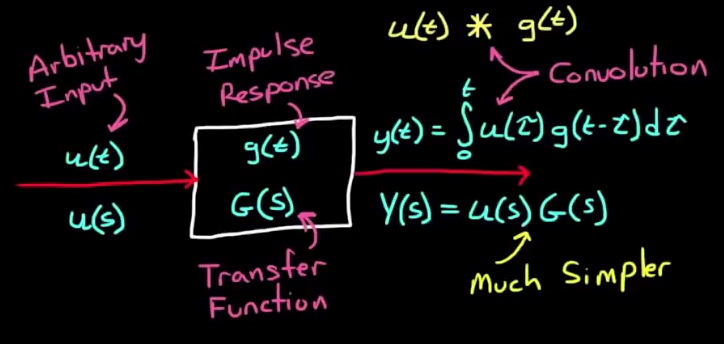
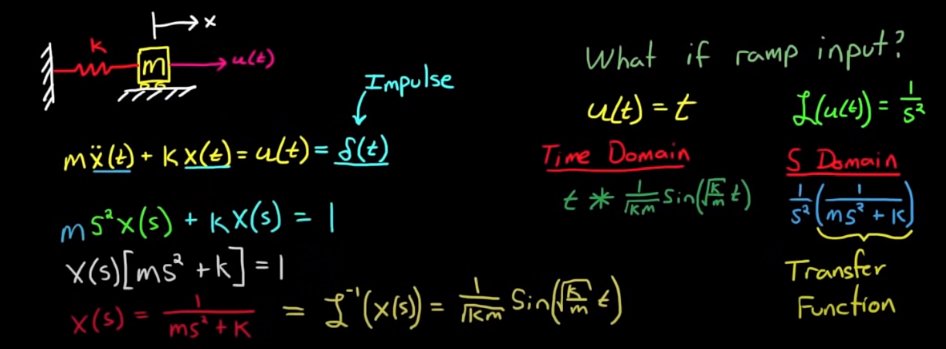
Let take a step back to understand this picture. In this case, $u(t)$ is input, and $x(t)$ is output. If we take $u(t)=\delta (t)$, we should have $x(t)=X(t)$ at the output. Taking Laplace transformation both side of the equation, $X(s)$ becomes Transfer function of the system.
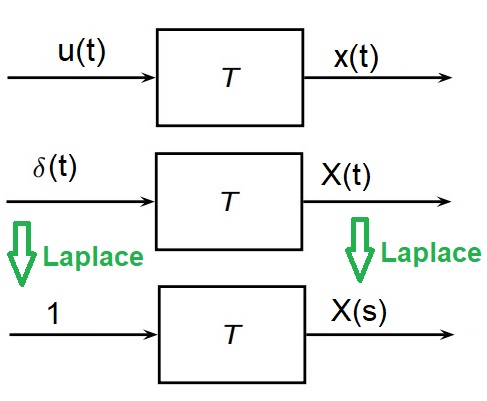
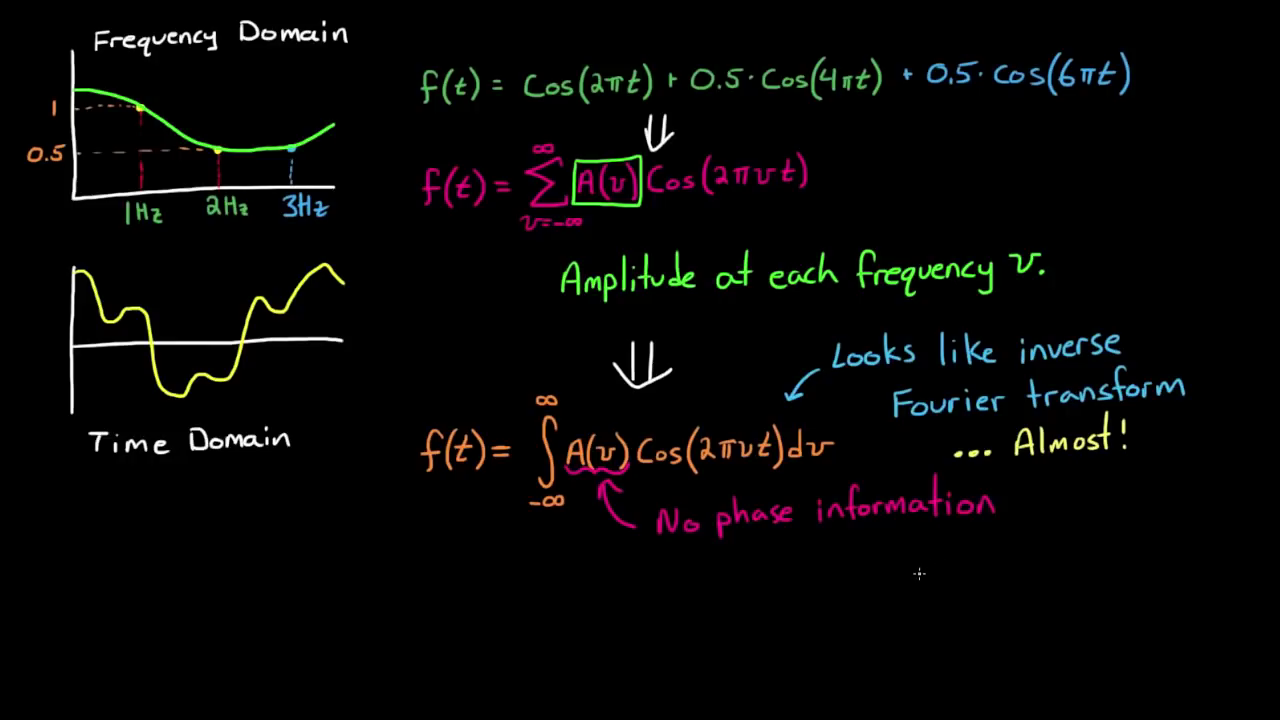
3. Fourier transformation
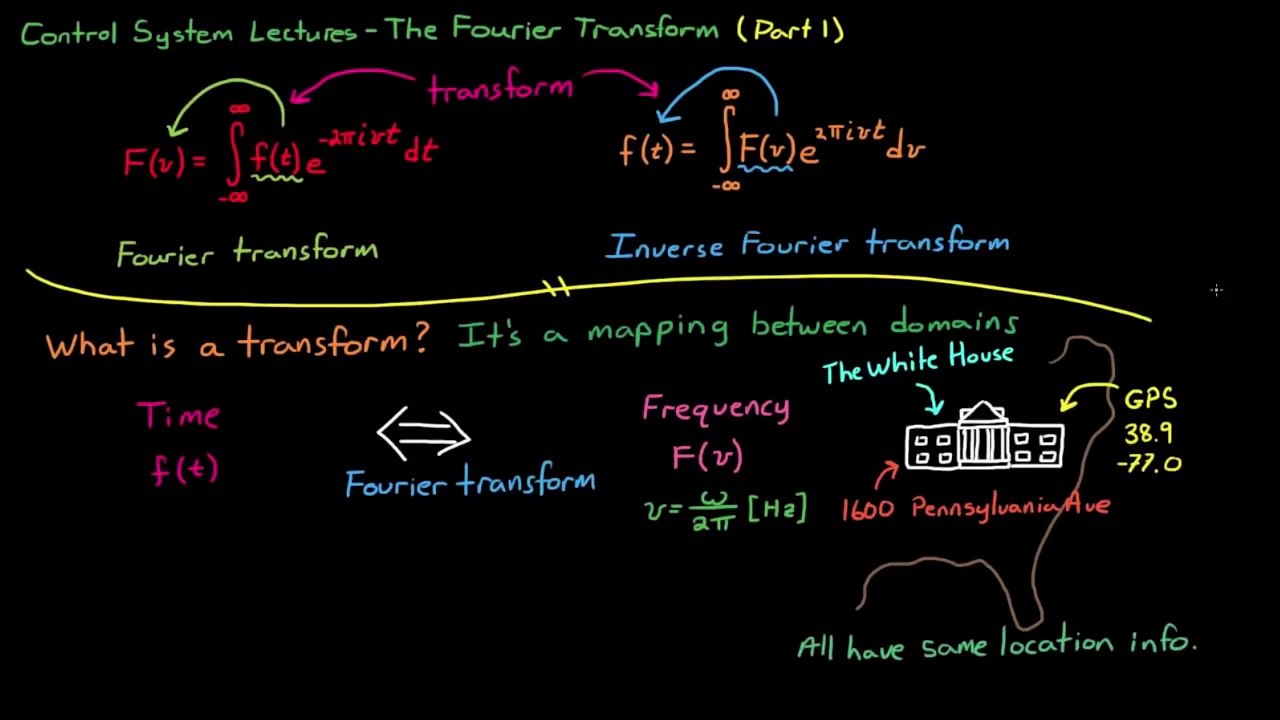
Q. Why sinusoidal?
A. Because its shape is the same in the LTI system. We only need to care about amplitude $A$ (i.e. Gain) and phase $\Phi$.
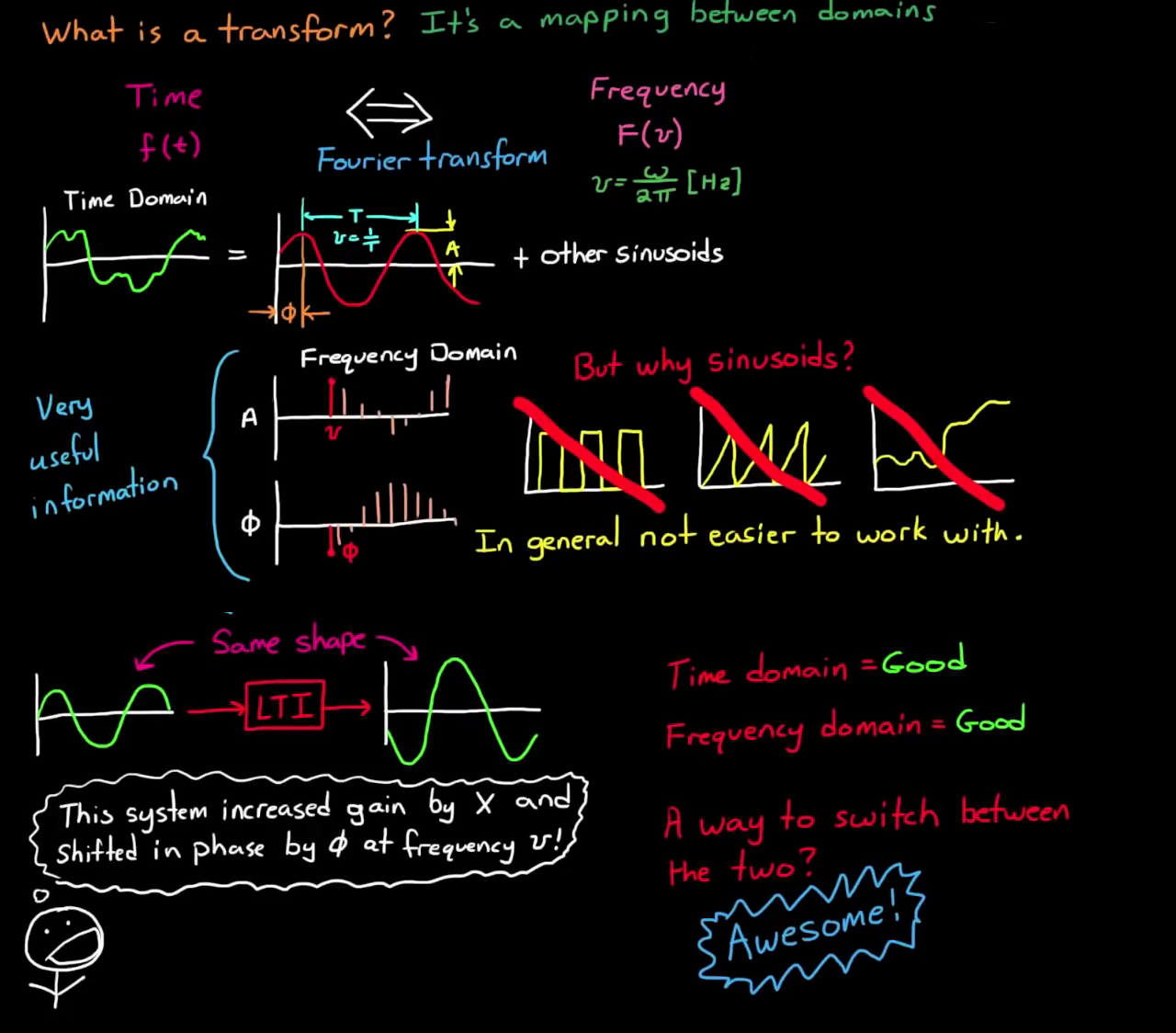
No phase information included.
Using complex number to include phase information into account.
