The fundamental of DC-AC inverter

Tuyen D. Le January 13, 2022 [Power-Electronics] #DC-AC

Refer ¹ for more details.

Getting started

Switch utilization

$$ \frac{P_o}{P_T} = \frac{V_{o1,max} \times I_{o1,max}}{q \times V_T \times I_T} $$

Where

$V_{o1,max}, I_{o1,max}$ are the maximum rated output voltage and current.
$V_T, I_T$ are the peak voltage rating and peak current rating of a switching device.
$q$ is the number of switches.

1. Full-brige inverters

TL;DR

Unipolar by definition: having or oriented in respect to a single pole.
Bipolar by definiton: having or involving the use of two poles or polarities.

$\begin{align*} & \text{Control signal: } V_{control}(t) = 𝑀 \times sin(\omega t) \\ & \text{Carrier signal: } V_{tri}(t) = \left\{\begin{matrix} \cfrac{4}{T_{sw} t} \qquad t \in [0,\cfrac{T_{sw}}{4}] \cup [\cfrac{3T_{sw}}{4},T_{sw}] \\ -\cfrac{4}{T_{sw} t} +2 \qquad t \in [\cfrac{T_{sw}}{4},\cfrac{3T_{sw}}{2}] \end{matrix}\right. \\ & \text{Output peak voltage } V_{out} = M \times V_{DC} \end{align*}$

Where:

$M$ is mudulation index.
$\omega$ is fundamental frequency.
$f_{sw} = 1 / T_{sw}$ is switching frequency.

Refer to ² for LTspice simulation instruction.

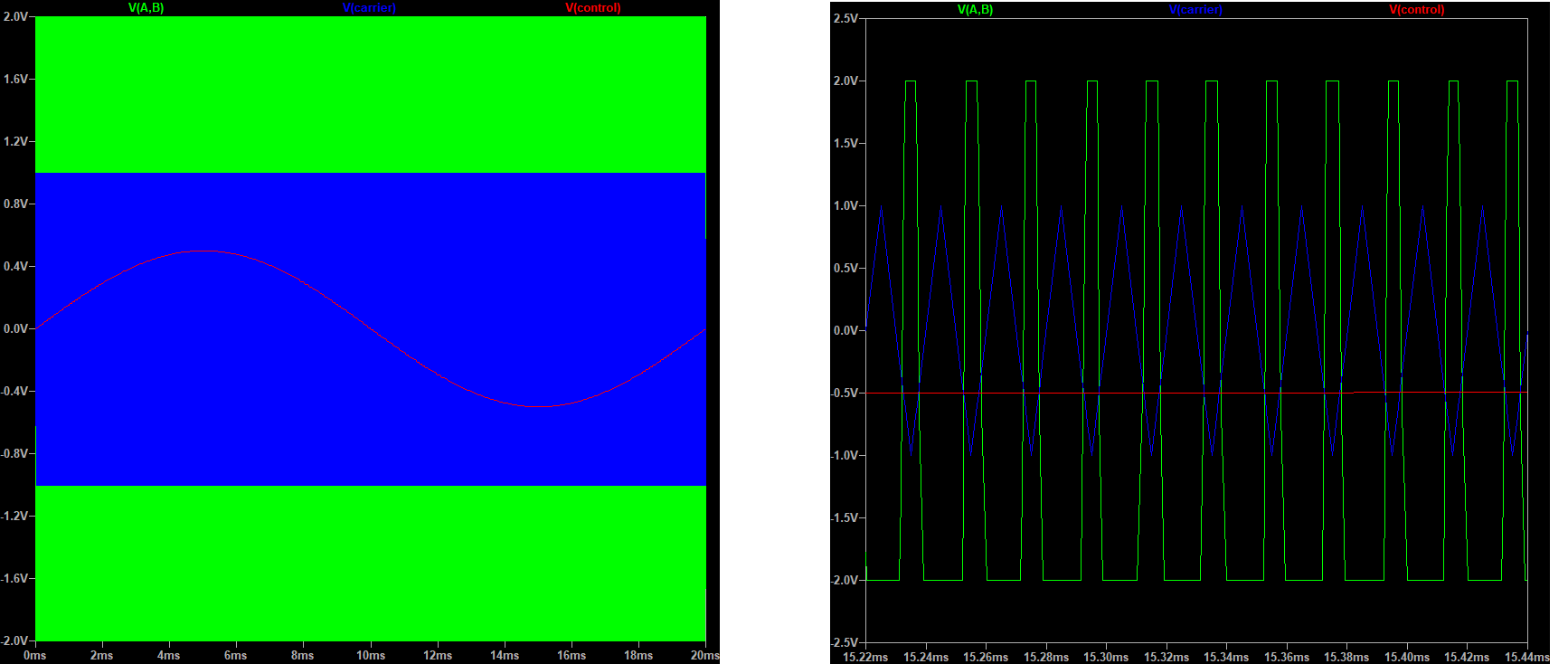
1.1. Biploar PWM

S1 and S4 turn on and turn off at the same time.

bipolar-PWM

Simulation result: bipolar-PWM-waveform

1.2. Unipolar PWM

The inverter output voltage switches between either between $0 \rightarrow +Vd$ during half cycle and $0 \rightarrow -Vd$ half cycle of the fundamental frequency thus this scheme is called unipolar modulation.

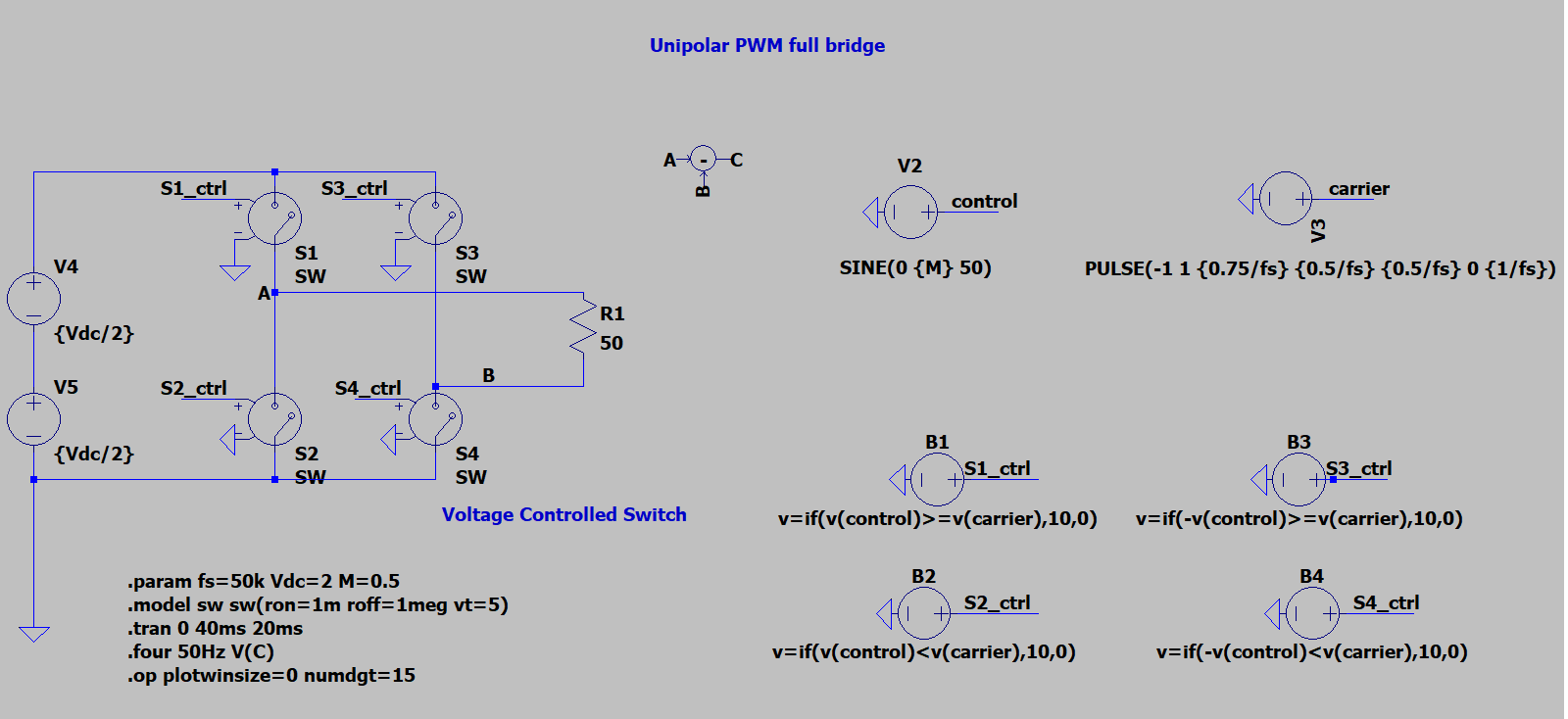
Unipolar PWM schematic

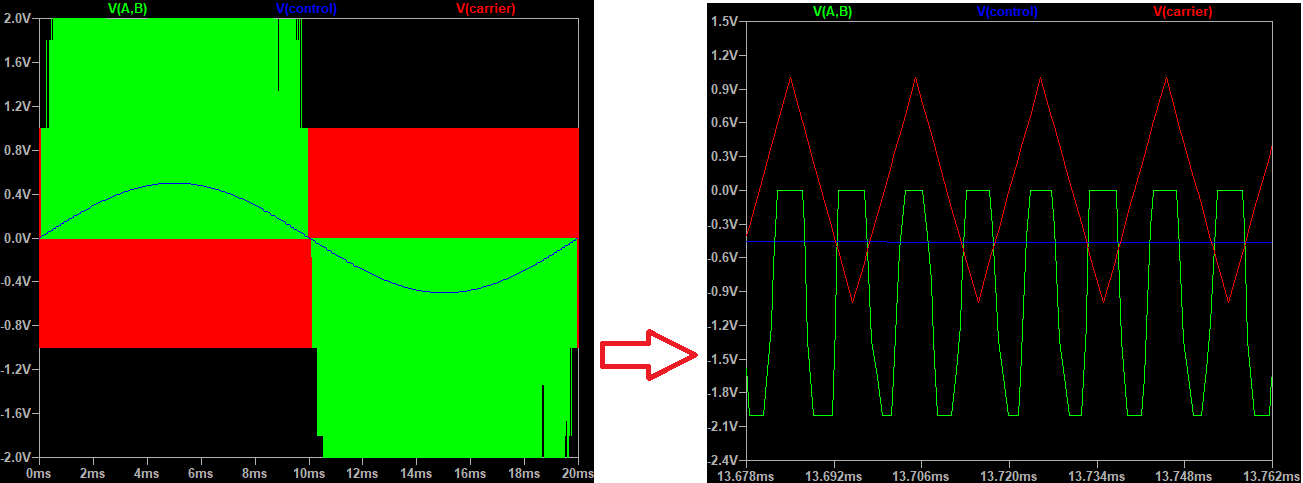
Unipolar PWM waveform

1.3. Hybrid PWM

Refer to ³

References

³: Lai, R.S. and Ngo, K.D., 1995. A PWM method for reduction of switching loss in a full-bridge inverter. IEEE Transactions on Power Electronics, 10(3), pp.326-332.

2. Vector space and three-phase inverter

3. Power losses and heating design of an DC-AC inverter

Power losses of an inverter is defined as

$$ P_{Loss} = P_{in} - P_{out} $$

We could measure the losses in two ways.

Direct measure $P_{in}$ and $P_{out}$. The stability of this method is difficult to achieve. A small variant in input or output could lead to a large error.
Indrect by using Calorimetric methos. Highest accuracy is achieved, but it is complicate to operate.

A alternative of measuring the losses is deriving the losses. The losses can be calculated by estimate of 4 types of power losses.

Switching losses
Conducting Losses
Blocking losses (neglecgable)
Driving losses (neglecable)

The rule of thumb for a good design is 50% of switching losses and 50% of conducting losses. Let take a closer look at the three-phase inverter.

three phase inverter

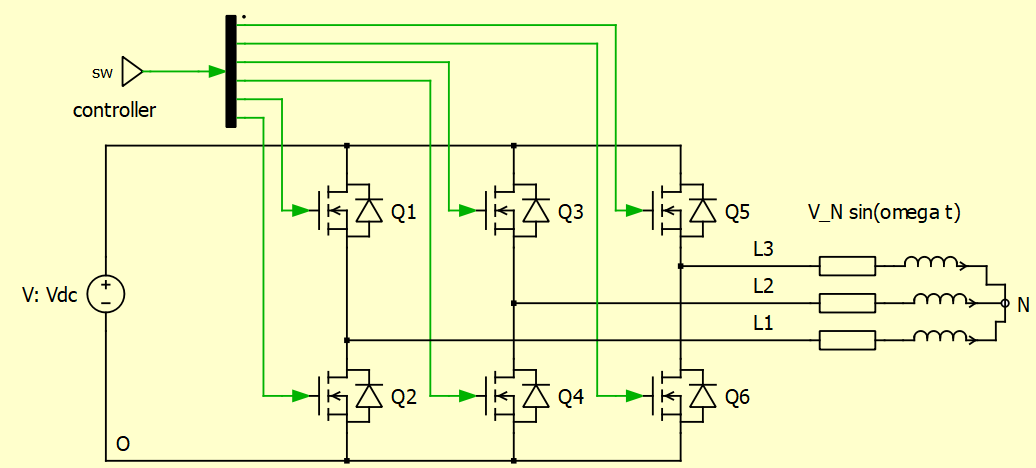
$$ P_{conduction} = \frac{1}{2 \pi} \int_{0}^{2 \pi} v (\omega t) i (\omega t) dt $$

Power switch is only conducting for half of period.

$\begin{align*} & P_C^{IGBT} = \frac{1}{2 \pi} \int_{0}^{\pi} \left[ V_{CE,0} \cdot i_{IGBT}(\omega t) + R_{CE} \cdot i_{IGBT}^2 (\omega t) \right] dt \\ & P_C^{MOSFET} = \frac{1}{2 \pi} \int_0^{\pi} \left [ r_{ds} \cdot i_{MOS}^2 (\omega t) \right ] dt \\ & P_C^{Diode} = \frac{1}{2 \pi} \int_0^{\pi} \left [ V_{Forward} \cdot i_{diode} (\omega t) + R_F \cdot i_{diode}^2 (\omega t) \right] dt \end{align*}$

$$ \text{Note: } V_{CE,0}, ; R_{CE}, ; R_{DS}, ;V_{F,0}, ; R_{F} \text{ are from the datasheets of Mosfet/IGBT/Diode.} $$

Using Kirchhoff's current law, we have,

$$ i_{IGBT} (\omega t) + i_{Diode} (\omega t) = \hat{i}_N ; sin(\omega t) $$

where:

$\begin{align*} & i_{IGBT}(\omega t) = m_{IGBT} (\omega t) \cdot \hat{i}_N \; sin(\omega t) \qquad (1) \newline & i_{Diode}(\omega t) = m_{Diode} (\omega t) \cdot \hat{i}_N \; sin (\omega t) \end{align*}$

In case of Sine-triangle PWM modulation, modulation function $m = M \cdot sin(\omega t + \phi)$ with $M$ is modulation index.

$\begin{align*} & m_{IGBT} - m_{Diode} = m \qquad (2) \\ & m_{IGBT} + m_{Diode} = 1 \end{align*}$

we have,

$\begin{align*} &m_{IGBT} = \frac{1+m}{2} = \frac{1}{2} \left( 1 + M \cdot sin(\omega t) \right) \qquad (3) \\ &m_{Diode} = \frac{1-m}{2} = \frac{1}{2} \left( 1 - M \cdot sin(\omega t) \right) \end{align*}$

Replace equation (1) by equation (3) we get,

$i_{IGBT} (\omega t) = \frac{1}{2} \left[ 1 + M \cdot sin(\omega t) \right] \hat{i}_N \; sin(\omega t) \newline i_{Diode} (\omega t) = \frac{1}{2} \left[ 1 - M \cdot sin(\omega t) \right] \hat{i}_N \; sin(\omega t)$

Finally, we get the important formular for conduction losses.

$\begin{align*} & P^{IGBT}_{C} = \frac{\hat{i_N} \cdot V_{CE,0}}{2 \pi} \left( 1 + \frac{M \cdot \pi}{4} cos \phi \right) + \frac{R_{CE} \cdot \hat{i_N}^2}{2 \pi} (\frac{\pi}{4} + \frac{2M}{3} cos\phi) \newline & P^{MOS}_C = \frac{R_{DS} \cdot \hat{i_N}^2}{2 \pi} (\frac{\pi}{4} + \frac{2M}{3} cos\phi) \qquad (V_{CE,0} = 0) \newline & P^{Diode}_C = \frac{\hat{i_N} \cdot V_{F,0}}{2 \pi} \left( 1 - \frac{M \cdot \pi}{4} cos \phi \right) + \frac{R_{F} \cdot \hat{i_N}^2}{2 \pi} (\frac{\pi}{4} - \frac{2M}{3} cos\phi) \end{align*}$

Since $R_{DS} \gg R_{CE}$, we could say that $P_C^{MOS}$ is not smaller than $P_C^{IBGT}$.

Switching losses

$$ \begin{align*} & P_{SW,IGBT} = \frac{1}{\pi} f_{SW} (E_{on} + E_{off}) \frac{V_{DC}}{V_{ref}} \frac{\hat{i_N}}{i_{ref}} \ & P_{SW,Diode} = \frac{1}{\pi} f_{SW} E_{rec} \frac{V_{DC}}{V_{ref}} \frac{\hat{i_N}}{i_{ref}} \ & \text{ where } E_{rec} = \frac{1}{2} V_{rr} \times Q_{rr} \end{align*} $$

4. References

David Perreault. 6.334 Power Electronics. Spring 2007. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.

Simulation of Bridge Inverter in LTspice

MOSFET Power Losses Calculation Using the DataSheet Parameters

Back to top