Complex number and its application in AC analysist

Tuyen D. Le February 10, 2022 [Power-Electronics] #Utility

1. Sinusoidal time functions and complex number

1.1. Complex number recap

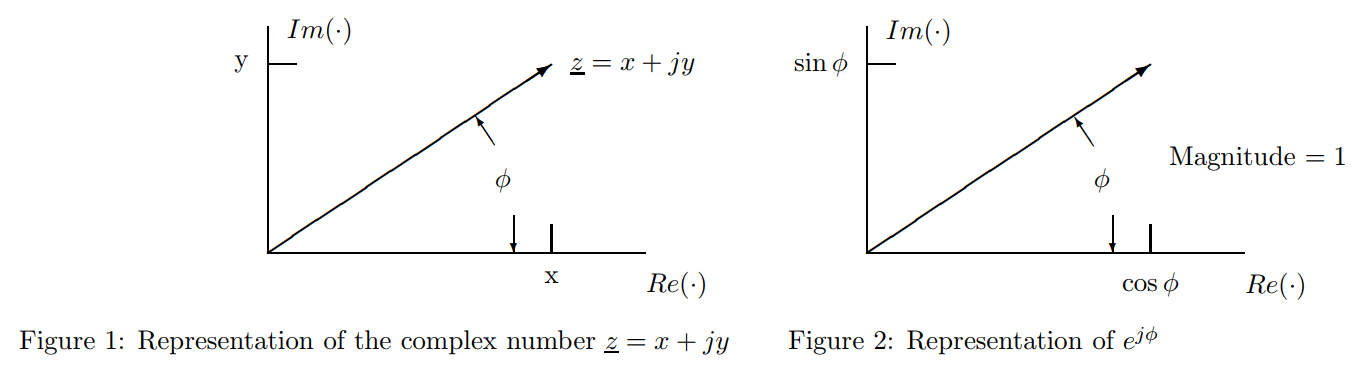
represenation of the complex number

Magnitude and phase angle of the complex number $\vec{z}$ is ¹

⚠️ Note:⚠️ The author was used $\underline{z}$ to denote a vector. However, I am using $\vec{z}$ to do this because of my personal preference.

$|\vec{z}|=\sqrt{x^{2}+y^{2}} \qquad \phi=\arctan \left(\frac{y}{x}\right)$

Euler relation

$e^{j \phi}=\cos (\phi)+j \sin (\phi) \qquad \vec{z}=x+j y=|\vec{z}| e^{j \phi}$

The product and the ratio of two complex numbers are

$\vec{z}_{1}=\left|\vec{z}_{1}\right| e^{j \phi_{1}} \qquad \vec{z}_{2}=\left|\vec{z}_{2}\right| e^{j \phi_{2}} \qquad \vec{z}_{1} \vec{z}_{2}=\left|\vec{z}_{1}\right|\left|\vec{z}_{2}\right| e^{j\left(\phi_{1}+\phi_{2}\right)} \qquad \frac{\vec{z}_{1}}{\vec{z}_{2}}=\frac{\left|\vec{z}_{1}\right|}{\left|\vec{z}_{2}\right|} e^{j\left(\phi_{1}-\phi_{2}\right)}$

The complex conjugate of a complex number is given by

$%  \vec{z}=x+j y \quad \vec{z}^{*}=x-j y \qquad \vec{z}+\vec{z}^{*}=2 \operatorname{Re}(\vec{z})=2 x \qquad \vec{z}-\vec{z}^{*}=2 j \operatorname{Im}(\vec{z})=2 j y$

1.2. Sinusoidal Time Functions

A sinusoidal function of time might be written in three ways

$f(t)=A \cos (\omega t+\phi) \qquad (1) \\ f(t)=B \cos (\omega t)+C \sin (\omega t) \qquad (2) \\ f(t)=\vec{X} e^{j \omega t}+\vec{X}^{*} e^{-j \omega t} \qquad (3)$

Equation (3) makes sure that that the resulting function is real. Now, let find out the relationship between equation (1) and (3).

Let say

$\vec{X}=|\vec{X}| e^{j \psi}$

then

$%  f(t) =|\vec{X}| e^{j \psi} e^{j \omega t}+|\vec{X}|^{*} e^{-j \psi} e^{-j \omega t} =|\vec{X}| e^{j(\psi+\omega t)}+|\vec{X}|^{*} e^{-j(\psi+\omega t)} \\ f(t)=2|\vec{X}| \cos (\omega t+\psi)$

so we have

$|\vec{X}| =\frac{A}{2} \qquad \psi =\phi$

Next, finding the relationship between equation (2) and (3).

Alternatively, we could write

$\vec{X}=x+j y \qquad \text{where} \quad x=|\vec{X}| \cos (\psi) \qquad y=|\vec{X}| \sin (\psi)$

thus

$f(t)=\vec{X} e^{j \omega t}+\vec{X}^{*} e^{-j \omega t} = x\left(e^{j \omega t}+e^{-j \omega t}\right)+j y\left(e^{j \omega t}-e^{-j \omega t}\right) \\ f(t) =2 x \cos (\omega t)-2 y \sin (\omega t)$

Finally, we get

$B = 2x \qquad C = -2y \qquad \vec{X} = \frac{B}{2} - j \frac{C}{2}$

1.3. Summary

Since

$%  (\vec{X} e^{j \omega t})^{*} = \vec{X}^{*} e^{-j \omega t}$

expression (3) and (4) are equivalent. It is advantageous to use one or the other of them, according to circumstances.
It's easy to notice that $\vec{X}$ is time-independent. This conclusion is used when forming the relationship between voltage and current of inductor and capacitor elements.

Sinusoidal form	Complex number form	$\vec{X}$
$f(t)=A \cos (\omega t+\phi)$	$f(t)=\vec{X} e^{j \omega t}+\vec{X}^{*} e^{-j \omega t} \quad (3)$	$\vec{X}={A}/{2} \angle \phi$
$f(t)=B \cos (\omega t)+C \sin (\omega t)$	$f(t)=Re(2\vec{X} e^{j \omega t}) = Re(A e^{j \phi} e^{j \omega t})\quad (4)$	$\vec{X} = {B}/{2} - j {C}/{2}$

Strategy:

Transform the input In into complex polar form $In \angle \phi$
Calculate impedance complex number $Z$
Transform output Out into polar form $O \angle \alpha$
Using expression (4) to find out $Out(t)$

2. Impedance

Consider two elements, inductances and capacitances.

Inducatance (L)	Capacitance (C)

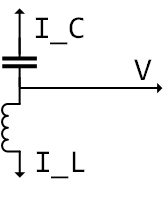Current is `lagging` voltage. (`L` means Lower :arrow_lower_right:)	Current is `leading` voltage
$v_L = L {di}/{dt}$	$i = C ; {dV_C}/{dt}$
$v = \vec{V}e^{j \omega t} + \vec{V}^{*} e^{-j \omega t}$	$i = \vec{I}e^{j \omega t} + \vec{I}^{*} e^{-j \omega t}$
$\vec{V}=j \omega L \vec{I} = \vec{Z}_L ; \vec{I} \quad \text{where } \vec{Z}_L = j \omega L$	$\vec{I}=j \omega C \vec{V} = \vec{V} / \vec{Z}_C \quad \text{where } \vec{Z}_C = 1 / (j \omega C)$

The inverse of impedance is admittance

$\vec{Y} = 1/ \vec{Z}$

Example

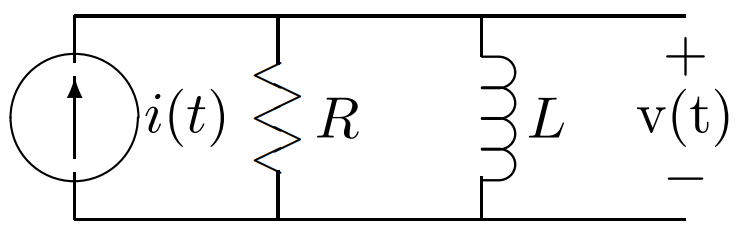
Suppose we are to find the voltage $v(t)$ in the network, in which $i(t) = I cos(\omega t)$ complex number in circuit example

Step 1. Transform the input In into complex polar form $In \angle \phi$

$i(t) = Re(I e^{\omega t})$

Step 2. Calculate impedance complex number $$ Z _| = \frac{R j \omega L}{R + j \omega L} = \frac{R \omega L}{\sqrt{R^2 + (\omega L)^2}} \angle (arctan \frac{R}{\omega L}) $$

phasor

Step 3. We found the output voltage in the polar-exponential form

$$ V = Z_| I = \frac{IR \omega L}{\sqrt{R^2 + (\omega L)^2}} \angle (arctan \frac{R}{\omega L}) $$

Step 4. Using expression (4) to find out $v(t)$

$$ v(t) = \frac{IR \omega L}{\sqrt{R^2 + (\omega L)^2}} cos ( \omega t + arctan \frac{R}{\omega L}) $$

References

James Kirtley Jr.. 6.061 Introduction to Electric Power Systems. Spring 2011. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.

Back to top